1. Pengertian Eksponen
Secara umum,
Eksponen biasa juga disebut dengan pangkat. Pada perpangkatan
1. Sifat-sifat eksponen:
Misalkan  , dan
, dan  adalah bilangan real, dengan
adalah bilangan real, dengan 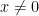 , maka:
, maka:
- Jika suatu bilangan dipangkatkan dengan 0, maka hasilnya adalah 1.
Sebagai contoh,,
, dan
.
Jadi, semua bilangan real (jika dipangkatkan dengan 0, hasilnya adalah 1.
- Jika suatu bilangan dipangkatkan dengan 1, maka hasilnya adalah
bilangan itu sendiri. Sedangkan jika 1 dipangkatkan dengan bilangan
berapa pun, hasilnya adalah 1.
Contoh:,
Jadi,dan
, berapa pun nilai x, dengan syarat x adalah bilangan real.
- Jika suatu bilangan dipangkatkan dengan bilangan negatif, berlaku sifat:
(sifat eksponen untuk pangkat negatif)
Contoh:
Contoh:atau
Contoh:
Contoh:(Sifat eksponen untuk pangkat pecahan)
Contoh:
Contoh:
2. Jika suatu bilangan dipangkatkan dengan 1, maka hasilnya adalah bilangan itu sendiri. Sedangkan jika 1 dipangkatkan dengan bilangan berapa pun, hasilnya adalah 1.
Contoh:
Jadi,
3. Jika suatu bilangan dipangkatkan dengan bilangan negatif, berlaku sifat:
Contoh:
2. Contoh Soal Eksponen
Soal 1: Tentukanlah bentuk sederhana dariJawab:
Perhatikan bahwa
Selanjutnya,
Terakhir,
Soal 2: Jika
Jawab:
Perhatikan bahwa setiap suku pada bentuk eksponen pecahan tersebut dapat kita nyatakan dengan bilangan pokok
Misalkan
Sekian pembahasan materi tentang eksponen, semoga membantu.
Sumber : http://www.sekolahmatematika.com/eksponen/
~Ani Syarah~
wah sangat membantu (y)
BalasHapus