Persamaan linear dua variabel adalah persamaan linear yang memiliki dua variabel, dengan pngkat masing masing variabel adalah satu. Persamaan Linear Dua Variabel memiliki bentuk umum yaitu :
ax + by = cx
dengan a,b dan c sebagai konstanta, x dan y sebagai konstanta.
Berikut ini beberapa contoh bentuk persamaan linear dua variabel lannya :
B. metode penyelesaian SPLDV
1. Metode Substitusi atau metode Mengganti
Metode subtitusi dapat di lakukan dengan menggantikan suatu variabel dengan variabel dari persamaan lain.
Contoh :
x – 2y = 4 ……..(i)
x + y = 10 ……..(ii)
Langkah awal
Ubahlah salah satu persamaan dalam bentuk X = ... Atau y = …
Dari persamaan (i), kita dapat memperoleh : x = 4 + 2y
Langkah kedua
Subtitusikan persamaan diatas ke perssamaan (ii) sehingga diperoleh :
x + y = 10
(4 + 2y) + y = 10
3y = 10 – 4
3y = 6
y = 2
Langkah Ketiga
Nilai y = 2 disubstitusikan ke persamaan (i) atau ke persamaan (ii).
Misalkan y = 2 disubtansikan ke persamaan(ii) diperoleh :
x + y = 10
x + 2 = 10
x = 10 – 2
x = 8
2. Metode Eliminasi atau metode menghilangkan
Metode eliminasi dilakukan dengan cara menghilangkan salah satu variabel. Contoh diatas dapat diselesaikan menggunakan metode eliminasi berikut.
Contoh :
x – 2y = 4 ……..(i)
x + y = 10 ……..(ii)
Langkah awal
mulailah dengan menghilangkan variabel x
x – 2y = 4
x + y = 10 -
-3 y = -6
y = 2
Langkah Kedua
hilangkan variabel y
x – 2y = 4 | x 1| x – 2y = 4
x + y = 10 |x 2 | 2x + 2y = 20 +
3x = 24
x = 8
3. Metode Campuran ( eliminasi dan substitusi )
Cara menyelesaikan sistem persamaan linear dua variabel dapat dilakukan dengan metode campuran dari eliminasi dan subtitusi.
Contoh :
x – 2y = 4 ……..(i)
x + y = 10 ……..(ii)
Langkah awal : metode eliminasi
hilangkan variabel x
x – 2y = 4
x + y = 10 -
-3y = -6
y =2
Langkah kedua : metode subtitusi
masukkan nilai y = 2 ke persamaan (i) atau ke persamaan ke (ii), misalkan nilai y = 2 dimasukkan ke persamaan (i).
x – 2y = 4
x – 2.2 = 4
x = 4 + 4
x = 8
jadi, penyelesaian sistem persamaan linear dua variabel diatas adlah x = 3 dan y = 0
C. contoh soal SPLDV
Jawab :
Luas taman = p x l
P = panjang taman
L = lebar taman
Model matematika :
P = 8 + l
k = 2p + 2l
2 ( 8 + l) + 2l = 44
16 + 2l + 2l = 44
16 + 4l = 44
4l = 28
l = 7
P = 7 + 8 = 15
Luas = 7 x 15 = 105 m2
Jadi, luas taman tersebut adalah 105 m2
~Ni Diah Ayu Putu~
ax + by = cx
dengan a,b dan c sebagai konstanta, x dan y sebagai konstanta.
Berikut ini beberapa contoh bentuk persamaan linear dua variabel lannya :
B. metode penyelesaian SPLDV
1. Metode Substitusi atau metode Mengganti
Metode subtitusi dapat di lakukan dengan menggantikan suatu variabel dengan variabel dari persamaan lain.
Contoh :
x – 2y = 4 ……..(i)
x + y = 10 ……..(ii)
Langkah awal
Ubahlah salah satu persamaan dalam bentuk X = ... Atau y = …
Dari persamaan (i), kita dapat memperoleh : x = 4 + 2y
Langkah kedua
Subtitusikan persamaan diatas ke perssamaan (ii) sehingga diperoleh :
x + y = 10
(4 + 2y) + y = 10
3y = 10 – 4
3y = 6
y = 2
Langkah Ketiga
Nilai y = 2 disubstitusikan ke persamaan (i) atau ke persamaan (ii).
Misalkan y = 2 disubtansikan ke persamaan(ii) diperoleh :
x + y = 10
x + 2 = 10
x = 10 – 2
x = 8
2. Metode Eliminasi atau metode menghilangkan
Metode eliminasi dilakukan dengan cara menghilangkan salah satu variabel. Contoh diatas dapat diselesaikan menggunakan metode eliminasi berikut.
Contoh :
x – 2y = 4 ……..(i)
x + y = 10 ……..(ii)
Langkah awal
mulailah dengan menghilangkan variabel x
x – 2y = 4
x + y = 10 -
-3 y = -6
y = 2
Langkah Kedua
hilangkan variabel y
x – 2y = 4 | x 1| x – 2y = 4
x + y = 10 |x 2 | 2x + 2y = 20 +
3x = 24
x = 8
3. Metode Campuran ( eliminasi dan substitusi )
Cara menyelesaikan sistem persamaan linear dua variabel dapat dilakukan dengan metode campuran dari eliminasi dan subtitusi.
Contoh :
x – 2y = 4 ……..(i)
x + y = 10 ……..(ii)
Langkah awal : metode eliminasi
hilangkan variabel x
x – 2y = 4
x + y = 10 -
-3y = -6
y =2
Langkah kedua : metode subtitusi
masukkan nilai y = 2 ke persamaan (i) atau ke persamaan ke (ii), misalkan nilai y = 2 dimasukkan ke persamaan (i).
x – 2y = 4
x – 2.2 = 4
x = 4 + 4
x = 8
jadi, penyelesaian sistem persamaan linear dua variabel diatas adlah x = 3 dan y = 0
C. contoh soal SPLDV
Penyelesaian sistem persamaan 3x –2y= 12 dan 5x + y = 7 adalah x = p dan y = q.
Nilai 4p + 3q adalah . . . .
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
Penyelesaian sistem persamaan 3x –2y= 12 dan 5x + y = 7 adalah x = p dan y = q.
Nilai 4p + 3q adalah . . . .
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
Penyelesaian sistem persamaan 3x –2y= 12 dan 5x + y = 7 adalah x = p dan y = q.
Nilai 4p + 3q adalah . . . .
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
1. Jika x dan y adalah penyelesaian dari sistem persamaan 7x + 2y = 19 dan 4x – 3y = 15, nilai 3x – 2y
adalah...
Eliminasi y:
7x + 2y
= 19 × 3 21x + 6y = 57
4x – 3y
= 15 × 2 8x – 6y = 30
––––––––––––
+
29x = 87
x =
3
Substitusi x = 3 ke persamaan 7x + 2y = 19:
7(3) + 2y =
19
21 + 2y =
19
2y = –2
y = –1
3x – 2y = 9 – (–2) = 9 + 2 = 11
Jadi, nilai 3x – 2y adalah 11.
Penyelesaian sistem persamaan 3x –2y= 12 dan 5x + y = 7 adalah x = p dan y = q.
Nilai 4p + 3q adalah . . . .
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
2. sebuah taman memiliki ukuran panjang 8
meter lebih panjang dari lebarnya. Keliling taman tersebut adalah 44 m.
tentukan luas taman !Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9
Penyelesaian sistem persamaan 3x –2y= 12 dan 5x + y = 7 adalah x = p dan y = q.
Nilai 4p + 3q adalah . . . .
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9v
Selengkapnya : http://www.kompasiana.com/suliezt/soal-dan-pembahasan-persamaan-liner-dua-variabel-spldv_54f3dedd745513a32b6c80f9v
Jawab :
Luas taman = p x l
P = panjang taman
L = lebar taman
Model matematika :
P = 8 + l
k = 2p + 2l
2 ( 8 + l) + 2l = 44
16 + 2l + 2l = 44
16 + 4l = 44
4l = 28
l = 7
P = 7 + 8 = 15
Luas = 7 x 15 = 105 m2
Jadi, luas taman tersebut adalah 105 m2
3. Harga 4 buah compact diskdan 5 buah kaset Rp200.000,00, sedangkan harga 2 buah compact disk dan 3
buah kaset yang sama Rp110.000,00. Harga 6 buah compact disk dan 5 buah
kaset adalah....
Misalkan x
= harga 1 buah compact disk
y
= harga 1 buah kaset
Harga 4 buah compact disk dan 5 buah kaset Rp200.000,00,
diperoleh persamaan:
4x + 5y = 200.000
Harga 2 buah compact disk dan 3 buah kaset yang sama
Rp110.000,00, diperoleh persamaan:
2x + 3y = 110.000
Diperoleh sistem persamaan:
4x + 5y = 200.000 . . . (1)
2x + 3y = 110.000 .
. . (2)
Eliminasi x
dari persamaan (1) dan (2).
4x +
5y = 200.000 × 1 4x + 5y =
200.000
2x +
3y = 110.000 × 2 4x + 6y =
220.000
–––––––––––––––
–
–y = –20.000
y =
20.000
Substitusikan y = 20.000 ke persamaan (2).
2x + 3y = 110.000
x + 3(20.000) = 110.000
2x + 60.000 = 110.000
2x = 110.000 – 60.000
2x = 50.000
x = 25.000
Diperoleh x = 25.000 dan y = 20.000.
Harga 6 buah compact disk dan sebuah kaset
= 6x + 5y
= 6 × 25.000 + 5 × 20.000
= 150.000 + 100.000
= 250.000
Jadi, harga 6 buah compact disk dan 5 buah kaset
Rp250.000,00.
Sekian pembahasan tentang sistem persamaan linear dua variabel, semoga bermanfaat.
~Ni Diah Ayu Putu~
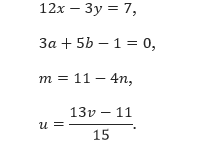
Tidak ada komentar:
Posting Komentar