A. Pengertian Lingkaran
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran, sedangkan jarak titik terhadap pusat lingkaran disebut jari-jari lingkaran.
Gambar dibawah ini menunjukkan lingkaran dengan pusat P dan jari-jari r.
B. Persamaan Lingkaran
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari-jari r
Pada lingkaran disamping jari-jari atau r = OP, OQ = x dan PQ = y.
Jarak dari O (0, 0) ke P (x, y) adalah.
Berdasarkan rumus Pythagoras
Jadi persamaan lingkaran dengan pusat O (0, 0) dan jari-jari r adalah x2 + y2 = r2
Contoh :
Tentukan persamaan lingkaran yang berpusat O (0, 0) dan jari-jari 5
Jawab :
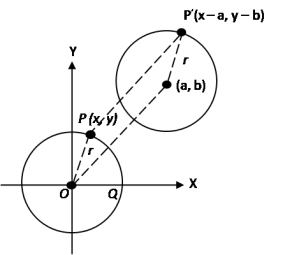
2. Persamaan lingkaran yang berpusat P (a, b) dan berjari-jari r
Persamaan lingkaran yang berpusat P(a, b) dan
berjari-jari r dapat diperoleh dari persamaan lingkaran yang
berpusat di (0, 0) dan berjari-jari r dengan menggunakan teori
pergeseran. Jika pusat (0, 0) bergeser (a, b) maka titik (x, y) bergeser ke (x + a, y + b).
Kita peroleh persamaan.
Persamaan lingkaran menjadi (x’– a)2 + (y’ – b)2 = r2
Jadi persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah
(x- a)2 + (y – b)2 = r2
Contoh :
Tentukan persamaan lingkaran berpusat di titik P(2, 3) yang melalui Q(5, -1)
Jawab :
Pusat (2, 3) maka a = 2 dan b = 3
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 2)2 + (y – 3)2 = 252
C. Bentuk Umum Persamaan Lingkaran
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah
(x- a)2 + (y – b)2 = r2
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2+ y2 – 2ax – 2by + a2+ b2– r2 = 0 atau x2+ y2 + Ax + By + a2+ b2+ C= 0
Jadi bentuk umum persamaan lingkaran x2+ y2 + Ax + By + a2+ b2+ C= 0
Contoh :
Tentukan pusat dan jari-jari lingkaran x2+ y2 – 4x +2y – 20= 0
Jawab :
A = -4, B = 2, dan C = -20
D. Kedudukan Titik Dan Garis Pada Lingkaran
1. Kedudukan Titik Pada Lingkaran
Letak K (m,n) terhadap X2+Y2 +Ax + By +C= 0 , ditentukan oleh nilai kuasa titik tersebut terhadap lingkaran
nilai kuasa K = m2+n2 +Am + Bn +C,
nilai kuasa K = m2+n2 +Am + Bn +C,
- K < 0 di dalam lingkaran
- K= 0 pada lingkaran
- K > 0 di luar lingkaran
Contoh 1:
Tentukan kedudukan titik-titik berikut terhadap lingkaran X2+y2 -8x -10y +16 =0 dan gambarlah
a. H(-3,9) b L(7,9), c M(10,5), d N(1,7)
Jawaban:Tentukan kedudukan titik-titik berikut terhadap lingkaran X2+y2 -8x -10y +16 =0 dan gambarlah
a. H(-3,9) b L(7,9), c M(10,5), d N(1,7)
- H(-3,9) K = (-3)2+92 -8.(-3) -10.9 +16 = 40, K > 0, diluar lingkaran
- L(7,9) K = (7)2+92 -8.(7) -10.9 +16 = 0, K = 0, pada lingkaran
- M(10,5) K = (10)2+52 -8.(10) -10.5 +16 = 11, K > 0, diluar lingkaran
- N(1,7) K = 12+72 -8.(1) -10.7 +16 = -12, K < 0, didalam lingkaran
Contoh 2:
Diketahui sebuah lingkaran X2+y2 -2x +6y -15 =0 dan sebuah titik S(m,1), tentukan batas nilai m agar
Diketahui sebuah lingkaran X2+y2 -2x +6y -15 =0 dan sebuah titik S(m,1), tentukan batas nilai m agar
- titik S didalam lingkaran
- titik S diluar lingkaran
| S(m,1) | = kuasa |
| = m2 +12 - 2m +6.1 - 15 | |
| = m2 - 2m - 8 |
| a. | Syarat di dalam lingkaran, K< 0 m2 -2m -8 <0 (m-4)(m+2)=0 |
| m=-2 atau m=4 | |
| didalam lingkaran jika -2 < m <4 ( daerah - - - ) | |
| diluar lingkran, K >0, jika m<-2 atau m >4 (daerah ++ ) |
2. Kedudukan Garis Pada Lingkaran
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Lihat diskriminannya: 
Jika
- D<0, berarti garis berada di luar lingkaran (tidak memotong lingkaran)
- D=0, berarti garis menyinggung lingkaran
- D>0, berarti garis memotong lingkaran di 2 titik berbeda.
Contoh 1:
- Tentukan posisi garis:
terhadap lingkaran
Jawab:
Karena  , maka garis berada di luar lingkaran.
, maka garis berada di luar lingkaran.
Contoh 2:
- Tentukan p agar garis
terletak di luar lingkaran
!
Jawab:
- syarat:
atau
jika di gambar dengan garis bilangan untuk pertidaksamaan diatas, maka akan didapatkan nilai p:  atau
atau 
Sekian pembahasan mengenai persamaan lingkaran, semoga membantu.
Sumber : http://tomyherawansman48jkt.blogspot.co.id/2015/06/persamaan-lingkaran-lingkaran-dengan.html
~Ni Diah Ayu Putu~

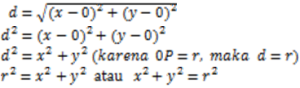
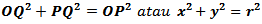
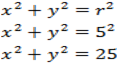
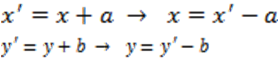
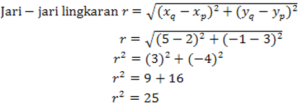
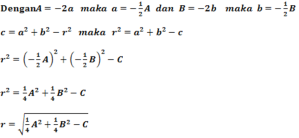

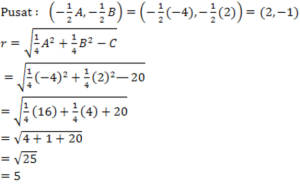
Tidak ada komentar:
Posting Komentar